Neural network can approximate wide variaty of functions when given “correct” parameters (weights). These parameters are trainable, we can adjust them to change results of neural net. The bigger network the more trainable parameters we can adjust in training process.

Universal approximation theorems imply that neural networks can represent a wide variety of interesting functions when given appropriate weights. Source

We will be calculating trainable parameters by hand so get some paper and pencil before we start. Every ML framework can calculate this for you, but how do they do that?

Calculating trainable params

At first we need some example net. We will use real pytorch code to get an idea what out neural net look like; see Fig 1.

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(400, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)
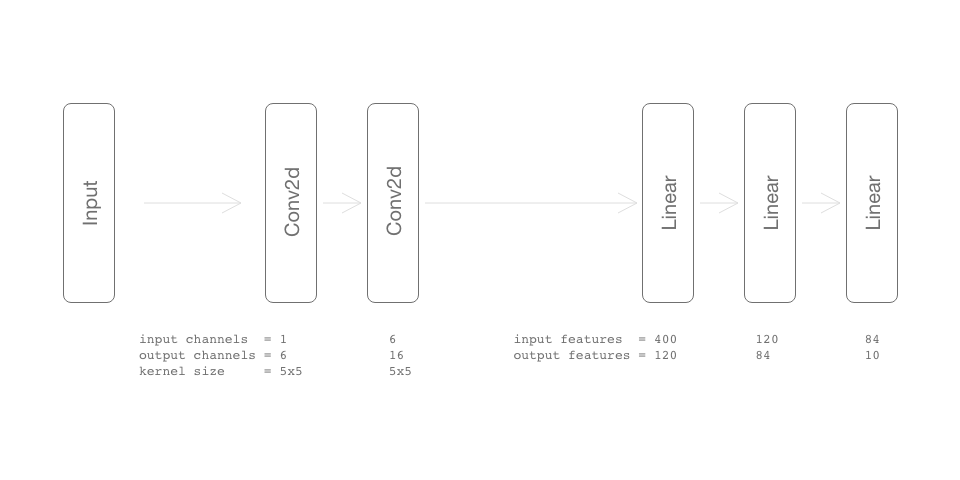
Fig 1.: Graphical representation of network architecture
Fig 1.: Graphical representation of network architecture

As you can see we don’t care if there is max pooling or what activation function is. Max pooling reduce dimensionality of tensors feature maps, but do not add trainable parameters.

Max pooling does not affect number of trainable parameters.
Fig 2.: Quick refresher about channels/feature maps. Channels and feature maps are representing same thing.
Fig 2.: Quick refresher about channels/feature maps. Channels and feature maps are representing same thing.

Number of params in convolution layers

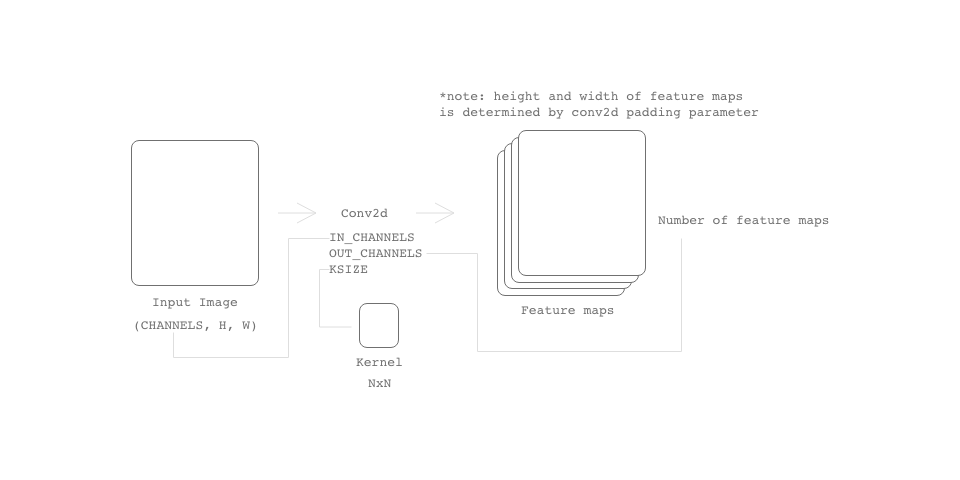
Let nn.Conv2d(1, 6, 5) be nn.Conv2d(IN_CHANNELS, OUT_CHANNELS, KSIZE). To get a better understanding of IN_CHANNELS/OUT_CHANNELS see Fig 2. Calculating all trainable params in one conv2d layer is as follows:

\[params = (KSIZE \cdot KSIZE \cdot IN\_CHANNELS + 1) \cdot OUT\_CHANNELS\]

Number of trainable params in our 2 conv2d layers:

\[(5\cdot5\cdot1+1)\cdot6 + (5\cdot5\cdot6+1)\cdot16 = 2572\]

The +1 stands for bias, for each output feature map we are adding one bias.

Number of trainable params in our 2 conv2d layers is 2572

Number of params in linear layers

Next we need to add up number of trainable params from linear layers.

This is much easier.

Let nn.Linear(400, 120) be nn.Linear(IN_FEATURES, OUT_FEATURES)

\[params = IN \cdot OUT + OUT\]

What does IN and OUT represent? IN are input connections to our linear layers and OUT is number of neurons in our linear layer. Each neuron also has bias therefore we need to add this number of biases to trainable params.

Number of trainable params in our 3 linear layers:

\[(400\cdot120 + 120) + (120\cdot84 + 84) + (84\cdot10+10) = 59134\]

Number of trainable params in our 3 linear layers is 59134

Last step is to sum number of params in all conv2d layers and linear layers.

\[59134 + 2572 = 61706\]

Calculating trainable params using pytorch

To calculate trainable params with pytorch you can use following snippet.

trainable_params = \
    sum(p.numel() for p in net.parameters() if p.requires_grad)